3.13 Coin guess without Bayes’ rule

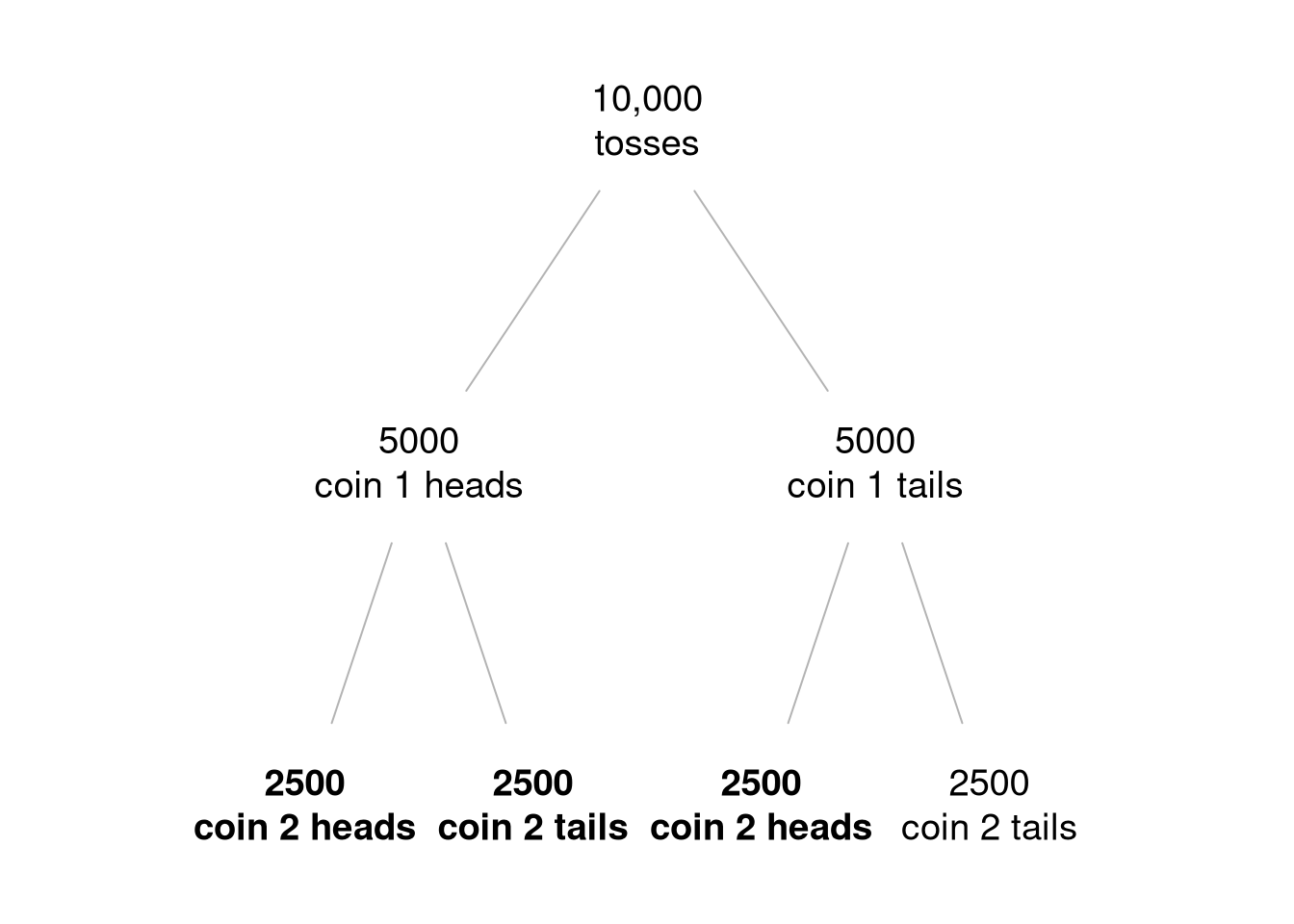
Figure 3.4: An expected frequency tree diagram of the coin guessing game. Outcomes other than double tails occur in 7500 out of the original 10,000 tosses (highlighted in bold). Out of those 7500 double tosses, 2500 came from coin 1 being tails, and 5000 came from coin 1 being heads. Since twice as many possible outcomes originate from coin 1 being heads the posterior odds of coin 1 being a head are 2:1.

Since a double tails did not occur, Player 2 knows that one of the following three outcomes must have occurred:

1. either coin 1 was a head and coin 2 was a head,
2. or coin 1 was a head and coin 2 was a tail,
3. or coin 1 was a tail and coin 2 was a head.

Figure 3.4 shows that for every 10,000 double tosses, the three outcomes above are expected in 7500 cases. In 5000 of these 7500, coin 1 is a head. In the other 2500, coin 1 is a tail. There are twice as many outcomes in which coin 1 is a head (5000 compared to 2500) and so the odds are 2:1 in favour of coin 1 being heads. These represent posterior odds, with the conditioning information being the fact that double tails has not occurred.

This means that player 2 should always guess a head when given the choice in this game, since the odds will be in their favour. This result might seem counter-intuitive at first glance. The key thing to understand is that the information that double tails has not occurred should update player 2’s belief about the possible outcomes of the tosses.