3.7 Example: double coin toss
Suppose now that we toss 2 coins, labelled coin 1 and coin 2. Coin 1 is tossed first and the outcome is recorded. Then coin 2 is tossed and its outcome is recorded. Both coins are tossed in such a way that guarantees a 0.5 probability of a head. The outcome of the toss of coin 1 can be used as conditioning information to see how it affects the probabilities of the outcomes of coin 2. This means that the uncertainty of interest is the toss of coin 2 conditioned on the outcome of the toss of coin 1. Question: what is the probability of getting a head with coin 2 after coin 1 has shown a head?
Conditioning information:
- coin 1 showing head
- background information - each coin has a 0.5 probability of a head.
With the above conditioning information the question becomes: is the outcome of coin 2 affected by the outcome of coin 1? If not, then the answer to the original question is 0.5 since the background information guarantees a 0.5 probability of a head for coin 2. The idea that the outcome of coin 2 is unaffected by the outcome of coin 1 is known as independence. This can sometimes be missed as an underlying unchecked assumption. It is helpful to add this to the background information so that the probability model is fully specified. All relevant assumptions can then be assessed by someone else.
Updated conditioning information:
- coin 1 showing head
- background information - each coin has a 0.5 probability of a head, tosses from coin 1 and 2 are independent of one another.
Figure 3.1 shows an expected frequency tree for this information for 10,000 tosses of the coins.
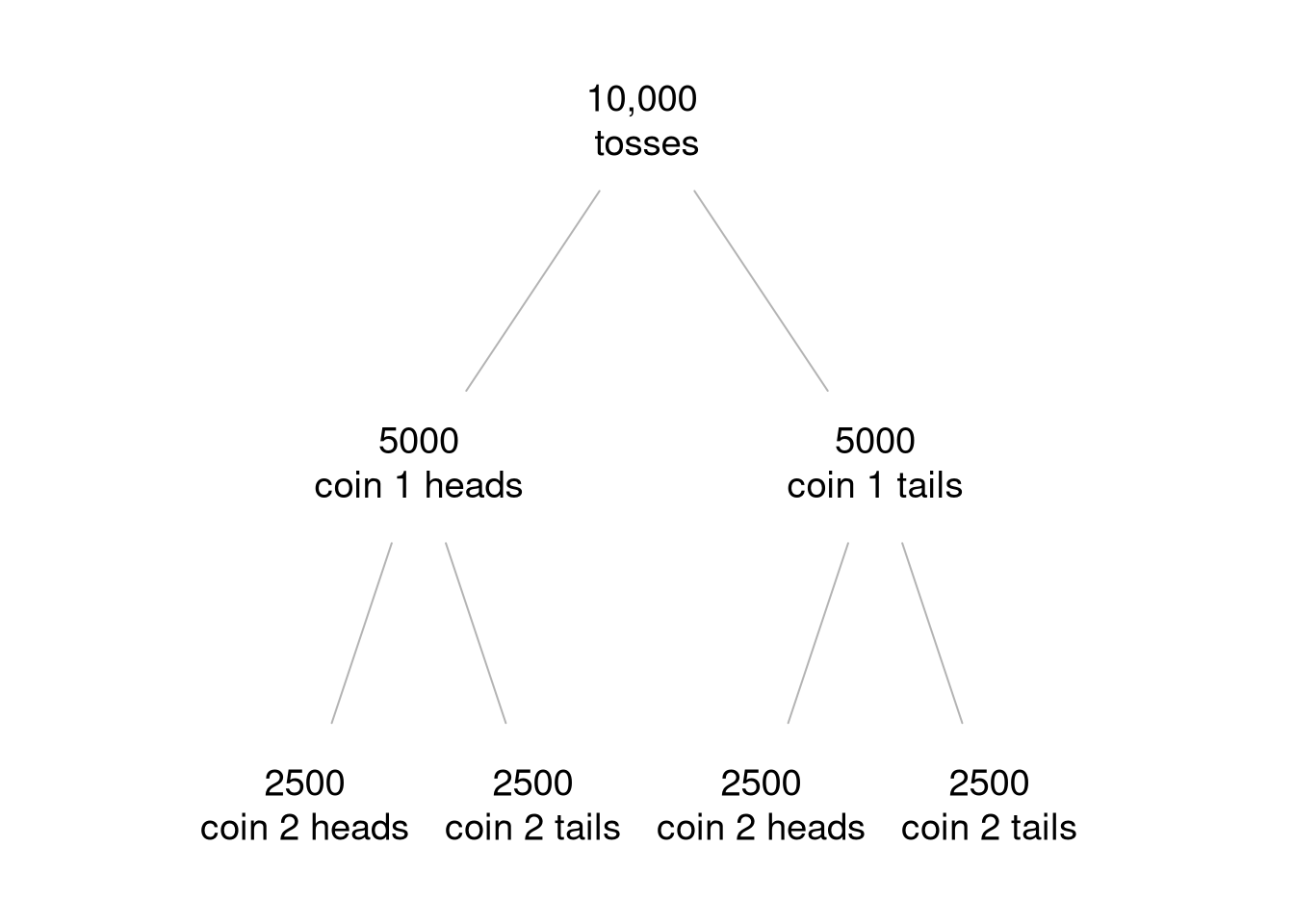
Figure 3.1: An expected frequency tree diagram of the double coin toss example. Out of every 10,000 double coin tosses, we expect 2500 to be double heads. The probability of getting two heads is 0.25.
After the 5000 tosses in which coin 1 is heads we expect 2500 heads from coin 2. This reflects the belief that coin 2 has a 0.5 probability of a head and is independent of coin 1.
The expected frequency tree can also help to answer other questions, such as: what is the probability of both coins showing a head? Out of the 10,000 tosses, 2,500 are expected to result in both coins showing heads. This reflects the belief that there is a \(\frac{2500}{10000}=\frac{1}{4}=0.25\) probability of obtaining a double heads.