3.9 Example: coin toss game
We can also consider two events for the same example which are not independent. Suppose there is a game that is decided by the result of the double coin toss. Player 1 wins if the coin tosses result in double heads and player 2 wins if the coin tosses result in double tails. If neither player wins then a draw is called and the coins are tossed again. Since double heads is just as likely as double tails, the probability is 0.25 for each, then both players are equally likely to win prior to the first coin being tossed. We can see this from the highlighted Figure 3.2 below.
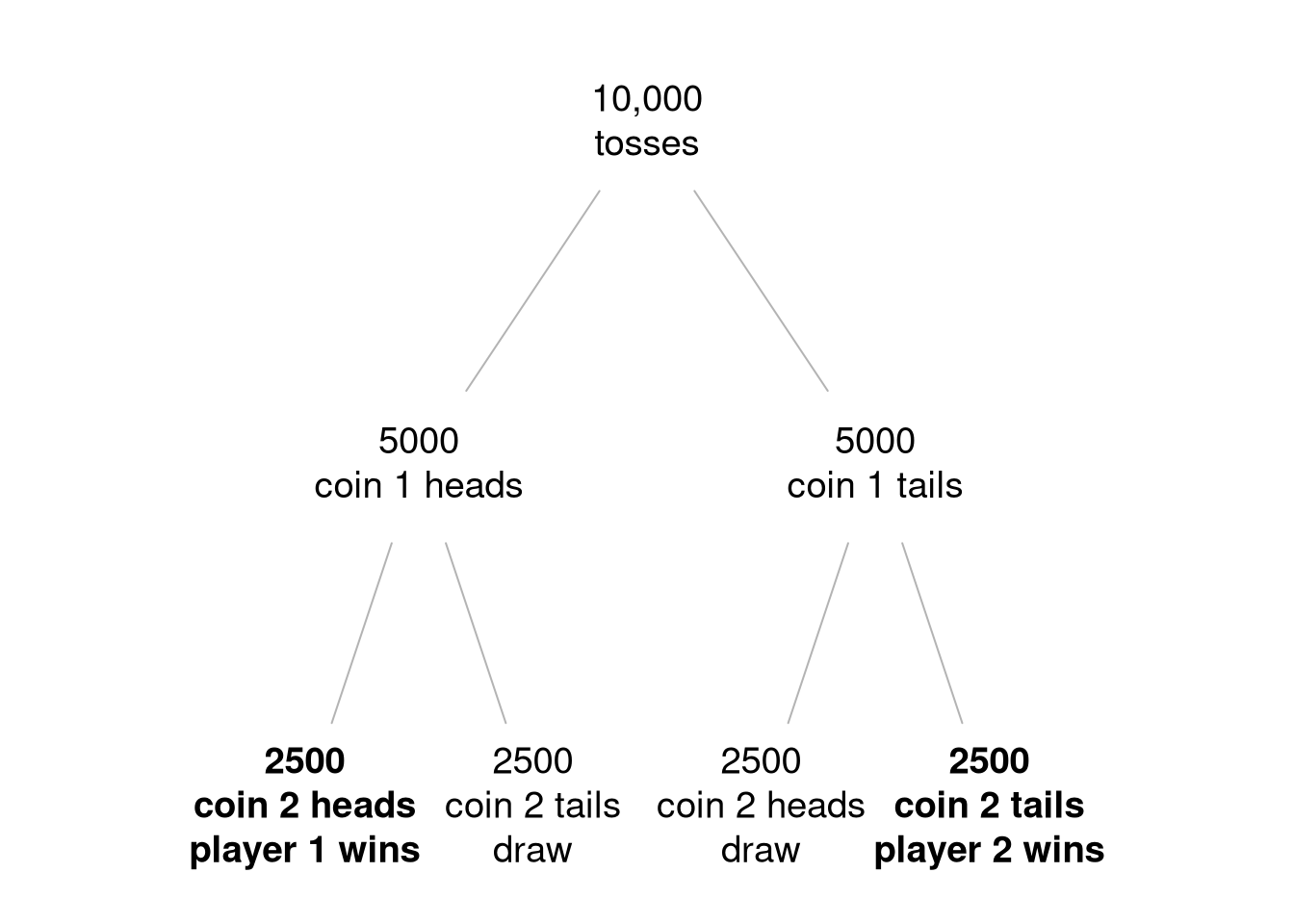
Figure 3.2: An expected frequency tree diagram of the double coin toss game. Out of every 10,000 tosses, 2500 are double heads and 2500 are double tails. This means that each player has equal an probability of winning of 0.25. The remaining 5000 tosses result in a draw and so the probability of a draw is 0.5.
Out of 10,000 double tosses, player 1 is expected to win 2500, player 2 is expected to win 2500, and 5000 double tosses are expected to result in a draw. However, whilst the outcome of coin 1 does not affect the outcome of coin 2, it does affect the winning probabilities for this game. For example, we can condition on coin 1 being a head as before.
Conditioning information:
- coin 1 showing head
- background information - each coin has a 0.5 probability of a head, tosses from coin 1 and 2 are independent of one another.
With the above conditioning information (i.e. only considering the left-hand branch of the tree), there is now a 0.5 probability that player 1 wins (2,500 out of 5,000), a 0.5 probability that there is a draw (2,500 out of 5,000), and it is impossible that player 2 wins in this round (0 out of 5,000). Conditioning on coin 1 being heads has increased the probability of player 1 winning from 0.25 to 0.5, and it has decreased the probability of player 2 winning from 0.25 to 0. The opposite occurs when the outcome of coin 1 is a tail. The probability of a draw remains unchanged at 0.5 before coin 1 is tossed, and 0.5 after it is tossed regardless of the result. In summary, the winning outcomes are not independent of the result of coin 1, but the draw is independent of it.