5.8 Doping LR
The likelihood ratio is given by \[\text{LR} = \frac{\text{probability of a positive test result assuming the athlete is doping}}{\text{probability of a positive test result assuming the athlete is not doping}}.\]
The conditional probabilities which contribute to this LR can be extracted from the expected frequency tree in which we assumed a population of 10,000 athletes, replicated in Figure 5.2.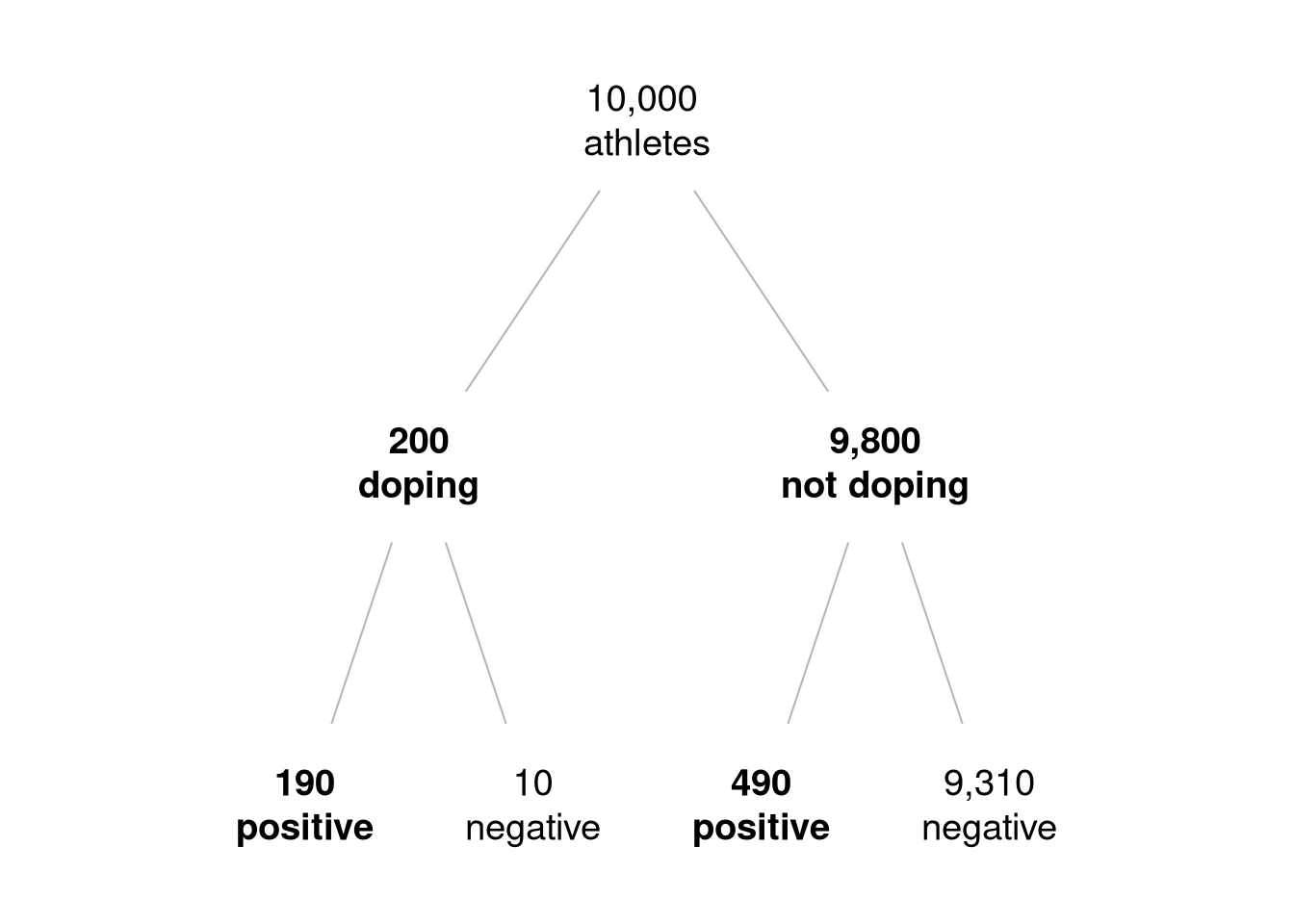
Figure 5.2: An expected frequency tree for the doping example. The terms which contribute to the LR of a positive test are those who test positive and this is shown in bold font.
For the numerator of the LR, “assuming that the athlete is doping” means that we are only looking at the branches of the tree for the doping athletes. We can see that 190 out of these 200 doping athletes test positive, a proportion of 0.95. This is given by the sensitivity of the test.
For the denominator of the LR, “assuming that the athlete is not doping” means that we only look at the branches of the tree for non-doping athletes. We can see that 490 out of the 9,800 non-doping athletes tested positive, a proportion of 0.05. This is given by 1 minus the specificity of the test.
The likelihood ratio in this example is equal to \(\frac{\text{sensitivity}}{1-\text{specificity}}=\frac{0.95}{0.05}=19\). The meaning of this can be expressed in a number of equivalent ways:
- a positive test result increases the prior odds that the athlete is doping by a factor of 19,
- a positive test result is 19 times more likely to be observed from doping athletes than from non-doping athletes,
- a positive test result provides 19 times more support for the proposition that the athlete is doping compared to not doping.
All of these expressions comment on the relative probability of observing a positive test result under the assumptions of the athlete doping and not doping. They do not state a value for the probabilities of the athlete doping or not, and they do not state that the athlete is 19 times more likely to be doping than not (this is an example of the prosecutor’s fallacy from Section 4.16).