3.12 Example: guessing coin 1

In this example we alter the double coin tossing game from Section 3.7. Suppose that player 1 now tosses the coins and hides the outcomes from player 2. After tossing the coins, player 1 only tells player 2 whether double tails were tossed or not. If double tails were tossed, then player 2 is given a chance to win by guessing the outcome of coin 1. If their guess is correct, then player 2 wins. Assume that the coins are tossed and player 2 is given the option to guess, what should their guess be?

Background information:

• player 1 tells the truth,
• player 1 tosses the coins in such a way that the odds are even for heads and tails for each coin,
• a double tails was not tossed (as this is why player 2 was given the option to guess).

This is a situation of epistemic uncertainty. Before the coin tosses, there is aleatory uncertainty - an unavoidable randomness to the future outcomes of these coin tosses. After the coin tosses, there is only epistemic uncertainty - player 1 knows the outcomes but player 2 does not.

Player 2 can use probabilities to make the best guess for the outcome of coin 1. The possible outcomes of the double coin toss are presented as an expected frequency tree in Figure 3.3 below.

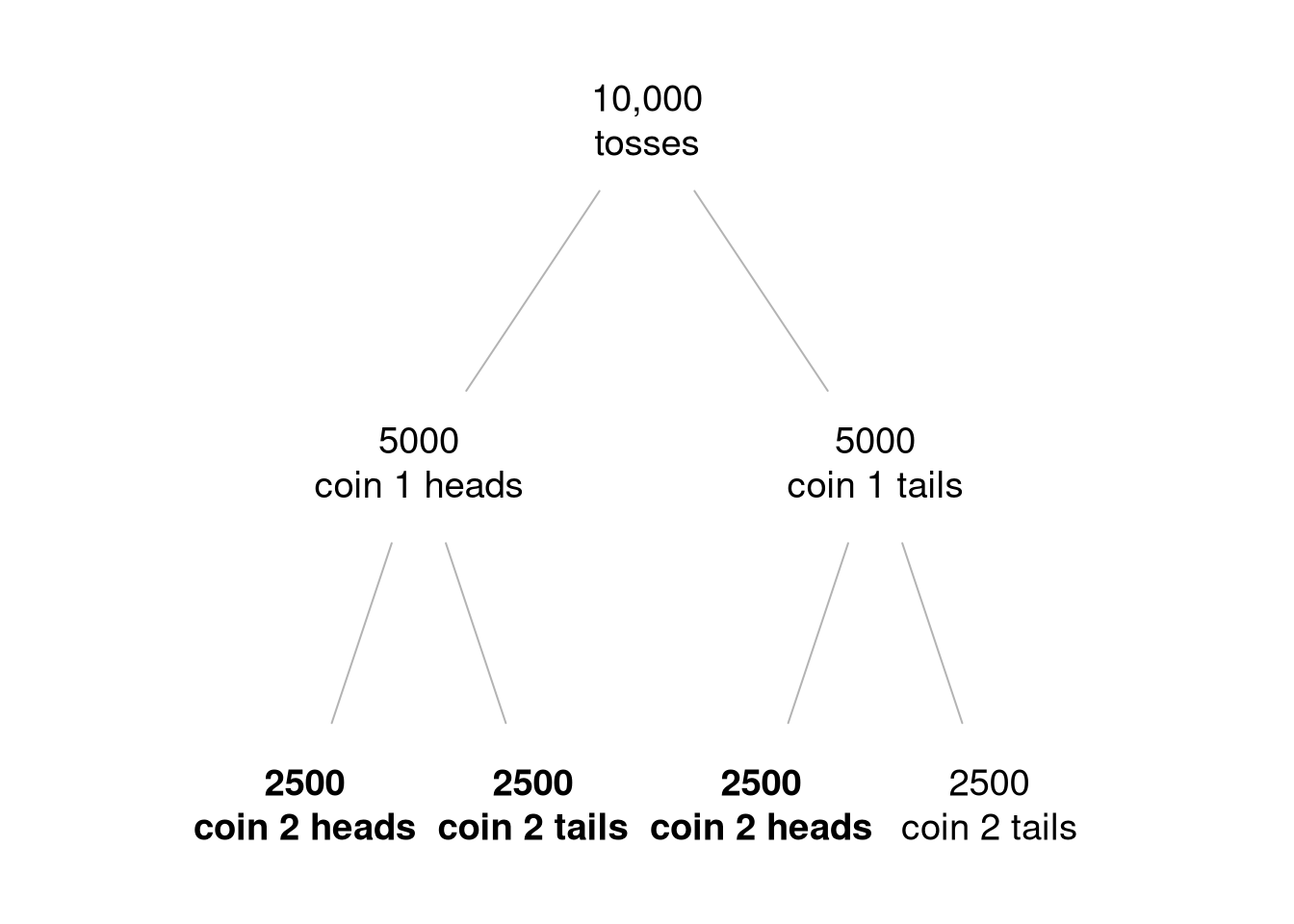
Figure 3.3: An expected frequency tree diagram of the coin guessing game. Outcomes other than double tails occur in 7500 out of the original 10,000 tosses (highlighted in bold).

The best guess can be logically reasoned both with and without using Bayes’ rule.